The problems based on this topic are nothing but puzzles in which letters take the place of digits in arithmetic operations and the task is to find the digits represented by the letters.
There
are three conditions to be satisfied to solve each puzzle, i.e.
(i)
Each letter represents only one digit.
(ii)
A number cannot begin with zero, e.g. forty-five is written as 45 but not as 045.
(iii)
A puzzle must have only one answer.
Example 1
Find the value of B and C in the following addition:
Solution:
We observe that a
certain single-digit number is added three times in which:
(i) the sum is a two-digit number; and
(ii) the given numbers
are B, B, B and the unit digit of the sum is also B.
It is something interesting. Right ?
So, let’s think like
this:
1 + 1 + 1 = 3
2 + 2 + 2 = 6
3 + 3 + 3 = 9
These three options
are not acceptable.
Reason: The sum is not a
two-digit number.
Now, think about the
following:
4 + 4 + 4 = 12
It has a two-digit sum
but it is also not acceptable.
Reason: The unit digit of the
sum is 2.
(Actually, 4 is expected. Right
?)
The next option is: 5 + 5 + 5 = 15
It has a two-digit
sum and it is ACCEPTABLE.
Reason: The unit digit of
the sum is 5 and this is expected too. Hurrah !
Now, what about the
following options ?
6 + 6 + 6 = 18
7 + 7 + 7 = 21
8 + 8 + 8 = 24
9 + 9 + 9 = 27
In each of the above, the sum is a two-digit number but the unit digit of the sum doesn’t satisfy the condition. So, these four options are also not acceptable.
Thus, the correct
option is: 5 + 5 + 5 = 15
Hence, C = 1 and B = 5.
Example 2
Find the value of A and B in the following addition:
Solution:
We observe that a
certain single-digit number is added three times in which:
(i) the sum is a two-digit number; and
(ii) the given numbers
are B, B, B and the unit digit of the sum is 4.
So, let’s consider the
following:
1 + 1 + 1 = 3
2 + 2 + 2 = 6
3 + 3 + 3 = 9
4 + 4 + 4 = 12
5 + 5 + 5 = 15
6 + 6 + 6 = 18
7 + 7 + 7 = 21
8
+ 8 + 8 = 24
9 + 9 + 9 = 27
We observe that 8 + 8
+ 8 = 24 satisfies both the conditions, i.e.
-
The sum is a two-digit number; and
-
The unit digit of the sum is 4.
Therefore, the correct
option is 8 + 8 + 8 = 24.
Hence, A = 8, B = 2.
PROBLEMS FOR PRACTICE
Question 1
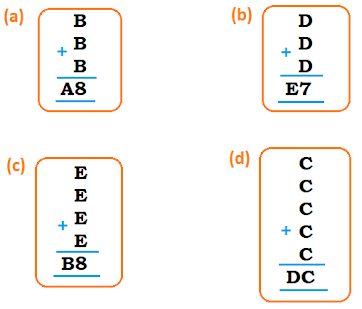
Find the value of the letters in each of the following. Give reason for the steps involved:
_________________________________________________________________
To be updated further..............




0 Comments